Regression

Danger

Do not use typical regression techniques for time-series data

Article to know how to evaluate whether a regression’s fit is good or not

Linear Regression

One of the most important algorithms in ML

Finds relationship between one or more independent variables and one dependent variable

Equation for line of best fit:

$f(x)={\beta }_{1}x+{\beta }_0$

Find values for ${\beta }_1$ and ${\beta }_0$ that minimize MSE (Mean Squared Error), which is the cost function:

$\mathrm{MSE}=\frac{1}{n}{\sum }_{i=1}^n(y_i-\widehat{y_i}{)}^2$

We use the square of the error because it’s easier to differentiate than the absolute value of the error

Residual: Difference between actual value and predicted value ($y-\hat{y}$)

Assumptions:

• Relationship must be linear
• Residuals must be independent - autocorrelation
• Residuals must be normally distributed
  • If not, you’re likely to have outliers
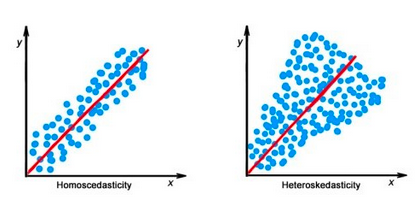
• Data must be homoscedastic, i.e., the variance in the outliers must be constant

$R^2$

Used to show how well line fits data (a measure of correlation)

Defined as 1 minus sum of the residuals squared divided by total sum of squares: $R^2=1-\frac{{\sum }_i(y_i-\widehat{y_i}{)}^2}{{\sum }_i(y_i-\bar{y}{)}^2}$

Ranges between -1 and 1:

• $R^2$ of 1 means perfect fit
• $R^2$ of 0 can happen if you just predict $\bar{y}$ (the mean) for every input
• $R^2$ of -1 means perfectly incorrect fit (negative $R^2$ not going to happen unless you screw up horribly)

RMSE

Our actual loss function

Good at comparing two models for same data

BUT is in the same units as whatever data we’re measuring, so useless on its own

$\mathrm{RMSE}=\sqrt{\frac{{\sum }_{i=1}^n({\mathrm{Predicted}}_i-{\mathrm{Actual}}_i{)}^2}{n}}$

Hypothesis Testing

We can perform a t-test to see how good our fit is

• Null hypothesis: Our slope is no better than 0
• Alternative hypothesis: Our slope is better than 0

Compare predicted values to actual values

Polynomial Regression

Prone to overfitting - generally only use it for smaller degree polynomials

Other types of regression

• Ridge regression: Does well with multicollinearity, where two independent variables are correlated
• Lasso regression: Useful when you have lots of potentially irrelevant features
• ElasticNet regression: Combines loss functions of ridge and lasso regression to get best of both worlds
• Random forest regression: In general, just do this first rather than messing around with the other types
  • Easy to use with minimal need for parameter tuning.
  • Generally reduces overfitting compared to single decision trees, in contrast to Ridge and Lasso, which focus on penalizing large coefficients.
  • Improved accuracy by aggregating predictions from multiple trees.
  • Can handle non-linearity, unlike Linear, Ridge, or Lasso regressions.
  • Robust against outliers by combining predictions from multiple trees, unlike Linear, Ridge, or Lasso regression.
  • Effective handling of large feature sets without extensive preprocessing.
  • Less sensitive to multicollinearity.